Analytical determination of a quasi-stationary electromagnetic field created by magnetic moments and eddy currents in conducting half-space
DOI:
https://doi.org/10.20998/2074-272X.2024.3.07Keywords:
three-dimensional quasi-stationary electromagnetic field, strong skin effect, external field of magnetic moments, asymptotic method, analytical solutionAbstract
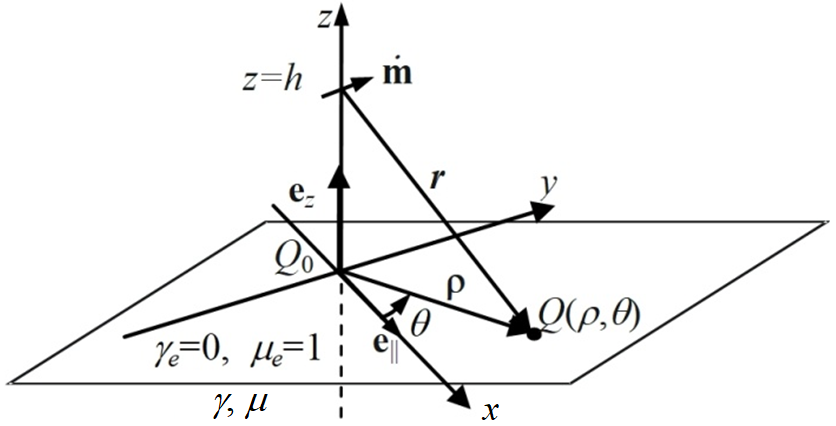
Aim. Study of the distribution of a three-dimensional alternating quasi-stationary electromagnetic field at the surface of conducting half-space with strong skin-effect, the source of which is an arbitrarily oriented magnetic moment. Methodology. The expressions for non-uniform electromagnetic field with strong skin effect are used for the analysis, which is based on the found exact analytical solution of the general three-dimensional problem and the use of expansion into asymptotic series with respect to a small parameter that is proportional to the ratio of the field penetration depth to the distance between the sources of the external field and the surface of body. Specific expressions at the surface are completely determined by the known field of external sources. In this work, the external magnetic moment field is used. Results. For strong skin effect, expressions for the electric and magnetic field strength are obtained separately for the components of the magnetic moment oriented perpendicularly and parallel to the flat surface between the dielectric and conducting areas. The features of the electromagnetic field distribution are analyzed depending on the value of introduced small parameter. The results are presented for the module and phase shift of the field strength with respect to the phase of the external field source. Originality. The expressions found for the electromagnetic field appear to be more general than the use of closed contours with alternating current, since they extend types of external field sources and allow the use of the superposition method instead of integration over the entire contour. Practical value. The found specific analytical expressions of the electromagnetic field at the surface for the external field of magnetic moments significantly simplify the solution of the problems, since they do not require additional solution of the field equations. References 20, figures 8.
References
Landau L.D., Lifshitz E.M. Electrodynamics of Continuous Media. Elsevier Ltd, 1984. 475 p. doi: https://doi.org/10.1016/B978-0-08-030275-1.50024-2.
Simonyi K. Foundation of Electrical Engineering. Elsevier Ltd, 1963. 865 p. doi: https://doi.org/10.1016/c2013-0-02694-1.
Leontovich M.A. On the Approximate Boundary Conditions for Electromagnetic Field on the Surface of Highly Conducting Bodies. Radio Wave Propagation Studies, 1948, pp. 5-12. (Rus).
Yuferev S., Ida N. Surface Impedance Boundary Conditions: A Comprehensive Approach. CRC Press, 2018. 412 p. doi: https://doi.org/10.1201/9781315219929.
Berdnik S.L., Penkin D.Y., Katrich V.A., Penkin Y. M., Nesterenko M.V. Using the concept of surface impedance in problems of electrodynamics (75 years later). Radio Physics and Radio Astronomy, 2014, vol. 19, no. 1, pp. 57-80. doi: https://doi.org/10.15407/rpra19.01.057.
Berdnyk S., Gomozov A., Gretskih D., Kartich V., Nesterenko M. Approximate boundary conditions for electromagnetic fields in electrodmagnetics. Radioelectronic and Computer Systems, 2022, no. 3, pp. 141-160. doi: https://doi.org/10.32620/reks.2022.3.11.
Vasetsky Y., Zaporozhets А. Electromagnetic Field Near Conducting Half-Space: Theory and Application Potentials. Lecture Notes in Electrical Engineering, 2023, vol. 1070, 124 p. doi: https://doi.org/10.1007/978-3-031-38423-3.
Vasetsky Y.M. Penetration of non-uniform electromagnetic field into conducting body. Electrical Engineering & Electromechanics, 2021, no. 2, pp. 43-53. doi: https://doi.org/10.20998/2074-272X.2021.2.07.
Vasetsky Y., Zaporozhets A. Approximate Mathematical Models for Analysis of Alternating Electromagnetic Field of Sources Near Conducting Body. Electromagnetic Field Near Conducting Half-Space. Lecture Notes in Electrical Engineering, 2023, vol. 1070, pp. 33-67. doi: https://doi.org/10.1007/978-3-031-38423-3_2.
Vasetskyi Y., Mazurenko I. Parameters for calculation of three-dimensional electromagnetic field by asymptotic expansion method. Computational Problems of Electrical Engineering, 2020, vol. 10, no. 1, pp. 37-44. doi: https://doi.org/10.23939/jcpee2020.01.037.
Nayfeh A.H. Introduction to Perturbation Techniques. Wiley-VCH, 1993. 536 p.
Smirnov V.I. A Higher Mathematics Course, Complex variables, special functions. vol. 3, part 2. Oxford, Pergamon Press, 1964. 700 p.
Rudnev V., Loveless D., Cook R., Black M. Handbook of Induction Heating. London, Taylor & Francis Ltd, 2017. 772 p. doi: https://doi.org/10.1201/9781315117485.
Lucia O., Maussion P., Dede E.J., Burdio J.M. Induction Heating Technology and Its Applications: Past Developments, Current Technology, and Future Challenges. IEEE Transactions on Industrial Electronics, 2014, vol. 61, no. 5, pp. 2509-2520. doi: https://doi.org/10.1109/TIE.2013.2281162.
Raschepkin A.P., Kondratenko I.P., Karlov O.M., Kryshchuk R.S. A method for calculating electromagnetic field of a spiral type induction system for magnetopulse processing of non-magnetic metal strips with a ferromagnetic shield. Technical Electrodynamics, 2022, no 2, pp. 43-51. (Ukr). doi: https://doi.org/10.15407/techned2022.02.043.
Lobanov L.M., Pashchyn M.O., Mykhodui O.L., Sydorenko Y.M. Effect of the Indenting Electrode Impact on the Stress-Strain State of an AMg6 Alloy on Electrodynamic Treatment. Strength of Materials, 2017, vol. 49, no. 3, pp. 369-380. doi: https://doi.org/10.1007/s11223-017-9877-1.
Polivanov K.M. Theoretical Bases of Electrical Engineers. Vol. 3. Theory of Electromagnetic Field. Moscow, Leningrad, Energiia Publ., 1965. 352 p. (Rus).
Tamm I.E. Fundamentals of the Theory of Electricity. Moscow, Mir Publ., 1979. 684 p. (Rus).
Novikov S.R., Fomenko A.T. Basic elements of differential geometry and torology. Springer, 1990. 500 p.
Theisel H., Rössl C., Weinkauf T. Topological Representations of Vector Fields. Mathematics and Visualization, 2008, pp 215-240. doi: https://doi.org/10.1007/978-3-540-33265-7_7.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Yu. M. Vasetsky

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Authors who publish with this journal agree to the following terms:
1. Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work.




