Determination of the maximum mechanical stresses in the insulating material around a defect with a high dielectric permittivity in an electrostatic field
DOI:
https://doi.org/10.20998/2074-272X.2024.1.09Keywords:
insulating material, internal and surface defect, electrostatics, structural mechanics, von Mises stress, finite element methodAbstract
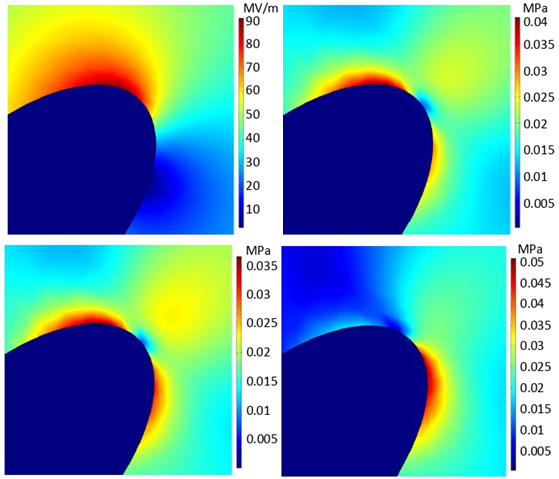
Introduction. All insulating macrohomogeneous solid materials change shape under the influence of an electric field. Problem. The presence of minor defects changes the distribution of an electric field and causes a significant concentration of mechanical stresses in a given section of the material, which, under certain circumstances, can cause partial or complete destruction of this material. Goal. The purpose of the work is to determine maximum mechanical stresses according to the von Mises criterion in insulating materials around defects with ionized air and water in an electrostatic field. Also, to analyze the influence of the following parameters on the indicated stresses: the location of the defect, the orientation angle of the semi-major axis of the defect cross-section, the ratio of semi-major and semi-minor axes, elastic and dielectric properties of the insulating material and the defect. Methodology. The study is based on the interrelated equations of electrostatics and structural mechanics for an isotropic piecewise homogeneous medium. The solution of these equations is obtained by the finite element method. Results. Graphs of dependences of maximum mechanical stresses on the ratio of semi-major and semi-minor axes of the ellipsoidal cross-section of the defect have been obtained. The minimum ratio of the greatest stresses in the insulating materials around the surface cracks and pores for ionized air has been 9.3 times for the maximum ratio of major and minor semi-axes of the cross-section of the defect considered in the work, which is 10. For a water defect, the similar ratio has been 2...5.6 times, increasing when the relative dielectric permittivity of the insulating material changes from 7 to 2. When Young’s modulus of the insulating material increases from 1 MPa to 100 GPa, the angles of the inclination of the linearized dependences of maximum mechanical stresses around bounded pores with ionized air (water) to the axis of the ratio of major and minor semi-axes of the defect cross-section have been increased by 35.9° (58.0°) and 18.6° (20.1°) at orientations of major semi-axes at angles of 0° and 45°, respectively. Originality. The numerical-field mathematical two-dimensional model has been developed for the first time, which consists of sequentially solved equations of electrostatics and structural mechanics, for the determination of the distribution of mechanical stresses in an insulating material with a liquid or gaseous defect. It has been established for the first time that the ratio of the elastic properties of the insulating material and the defect determines the angle of the inclination of the linearized dependence of the maximum mechanical stress to the axis of the ratio of major and minor semi-axes of the defect cross-section. Practical value. The types of defects that contribute to the aging of insulation materials under the combined action of an electric field and a stress field to the greatest extent have been established.
References
Zhou T., Zhu X., Yang H., Yan X., Jin X., Wan Q. Identification of XLPE cable insulation defects based on deep learning. Global Energy Interconnection, 2023, no. vol. 6, no. 1, pp. 36-49. doi: https://doi.org/10.1016/j.gloei.2023.02.004.
Qu Z., Zhang G., Fu Y., An Y., Chen C., Shan X. Defect detection for the insulation layer of bent aircraft cables based on ultrasonic guided waves. IEEE Transactions on Instrumentation and Measurement, 2023, vol. 72, pp. 1-8. doi: https://doi.org/10.1109/TIM.2023.3241040.
Zhou X., Tian T., Li X., Chen K., Luo Y., He N., Liu W., Ma Y., Bai J., Zhang X. and Zhang G. Study on insulation defect discharge features of dry-type reactor based on audible acoustic. AIP Advances, 2022, vol. 12, no. 2, art. no. 025210. doi: https://doi.org/10.1063/5.0078735.
Wang Y., Nie Y., Qi P., Zhang N., Ye C. Inspection of defect under thick insulation based on magnetic imaging with TMR array sensors. IEEE Transactions on Magnetics, 2021, vol. 58, no. 3, art. no. 6200510. doi: https://doi.org/10.1109/TMAG.2021.3138587.
Palchykov O.О. Breakdown voltage of micron range air inclusions in capacitor paper. Electrical Engineering & Electromechanics, 2020, no. 6, pp. 30-34. doi: https://doi.org/10.20998/2074-272X.2020.6.05.
Li G., Liang X., Zhang J., Li X., Wei Y., Hao C. Insulation properties and interface defect simulation of distribution network cable accessories under moisture condition. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, vol. 29, no. 2, pp. 403-411. doi: https://doi.org/10.1109/TDEI.2022.3157902.
Vavilova G., Yurchenko V., Keyan L. Influence of the insulation defects size on the value of the wire capacitance. Progress in Material Science and Engineering, Part of the Studies in Systems, Decision and Control book series (SSDC), 2021, no. 351, pp. 113-123. doi: https://doi.org/10.1007/978-3-030-68103-6_11.
Ndama A.T., Ndong E.O., Boussougou Y.C.M., Tsoumou G.J., Blampain E.J.J. Theoretical Study of Potential Manufacturing Insulation Defects in Medium–Voltage Traction Motors. International Journal of Emerging Technology and Advanced Engineering, 2022, vol. 12, no. 1, pp. 83-98. doi: https://doi.org/10.46338/ijetae0122_09.
Uydur C.C., Arikan J., Kalenderli Ö. The effect of insulation defects on electric and magnetic field distributions in power cables. Tehnicki Vjesnik, 2021, vol. 28, no. 4, pp. 1152-1160. doi: https://doi.org/10.17559/TV-20200205084232.
Han W., Yang G., Hao C., Wang Z., Kong D. and Dong Y. A data-driven model of cable insulation defect based on convolutional neural networks. Applied Sciences, 2022, vol. 12, no. 16, art. no. 8374. doi: https://doi.org/10.3390/app12168374.
Zeller H.R., Schneider W.R. Electrofracture mechanics of dielectric aging. Journal of Applied Physics, 1984, vol. 56, no. 2, pp. 455-459. doi: https://doi.org/10.1063/1.333931.
Scanavi G.I. Physics of dielectrics (region of strong fields). Moscow, GIFML Publ., 1958. 909 p. (Rus).
Blythe T., Bloor D. Electrical properties of polymers. Cambridge University Press, 2008. 496 p.
Zhou X., Zhao X., Suo Z., Zou C. Electrical breakdown and ultrahigh electrical energy density in poly (vinylidene fluoride-hexafluoropropylene) copolymer. Applied Physics Letters, 2009, vol. 94, no. 16, art. no. 162901. doi: https://doi.org/10.1063/1.3123001.
Karpov V.G., Kryukov Y.A., Karpov I.V., Mitra M. Field-induced nucleation in phase change memory. Physical Review B, 2008, vol. 78, no. 5, art. no. 052201. doi: https://doi.org/10.1103/PhysRevB.78.052201.
Montanari G.C., Seri P., Dissado L.A. Aging mechanisms of polymeric materials under DC electrical stress: A new approach and similarities to mechanical aging. IEEE Transactions on Dielectrics and Electrical Insulation, 2019, vol. 26, no. 2, pp. 634-641. doi: https://doi.org/10.1109/TDEI.2018.007829.
Ding H.-Z., Varlow B.R. Thermodynamic model for electrical tree propagation kinetics in combined electrical and mechanical stresses. IEEE Transactions on Dielectrics and Electrical Insulation, 2005, vol. 12, no. 1, pp. 81-89. doi: https://doi.org/10.1109/TDEI.2005.1394018.
Pallon L.K.H., Nilsson F., Yu S., Liu D., Diaz A., Holler M., Chen X.R., Gubanski S., Hedenqvist M.S., Olsson R.T., Gedde U.W. Three-Dimensional Nanometer Features of Direct Current Electrical Trees in Low-Density Polyethylene. Nano Letters, 2017, vol. 17, no. 3, pp. 1402-1408. doi: https://doi.org/10.1021/acs.nanolett.6b04303.
Kitani R., Iwata S., Imatani S. Energy-Release Rate in Electrically Deteriorated Materials Introduced by Using Maxwell Stress Tensor at Crack Tip. IEEE Transactions on Dielectrics and Electrical Insulation, 2021, vol. 28, no. 6, pp. 1925-1932. doi; https://doi.org/10.1109/TDEI.2021.009692.
Zuoqian Wang, Marcolongo P., Lemberg J.A., Panganiban B., Evans J.W., Ritchie R.O., Wright P.K. Mechanical fatigue as a mechanism of water tree propagation in TR-XLPE. IEEE Transactions on Dielectrics and Electrical Insulation, 2012, vol. 19, no. 1, pp. 321-330. doi: https://doi.org/10.1109/TDEI.2012.6148534.
Kucheriava I.M. Computer analysis of electromechanical stress in polyethylene insulation of power cable at available micro-inclusion. Technical Electrodynamics, 2012, no. 5, pp. 10-16. (Rus).
Podoltsev O.D., Kucheriava I.M. Multiphysics processes in the region of inclusion in polyethylene insulation of power cable (three-dimensional modeling and experiment). Technical Electrodynamics, 2015, no. 3, pp. 3-9. (Rus).
Bezprozvannych G.V., Mirchuk I.A. Correlation between electrical and mechanical characteristics of cables with radiation-modified insulation on the basis of a halogen-free polymer composition. Electrical Engineering & Electromechanics, 2018, no. 4, pp. 54-57. doi: https://doi.org/10.20998/2074-272X.2018.4.09.
Bezprozvannych G.V., Boyko A.N., Roginskiy A.V. Effect of a dielectric barrier on the electric field distribution in high-voltage composite insulation of electric machines. Electrical Engineering & Electromechanics, 2018, no. 6, pp. 63-67. doi: https://doi.org/10.20998/2074-272X.2018.6.09.
Bezprozvannych G.V., Kyessayev A.G., Mirchuk I.A., Roginskiy A.V. Identification of technological defects in high-voltage solid insulation of electrical insulation structures on the characteristics of partial discharges. Electrical Engineering & Electromechanics, 2019, no. 4, pp. 53-58. doi: https://doi.org/10.20998/2074-272X.2019.4.08
Abrate S. Criteria for Yielding or Failure of Cellular Materials. Journal of Sandwich Structures & Materials, 2008, vol. 10, no. 1, pp. 5-51. doi: https://doi.org/10.1177/1099636207070997.
Stratton J.A. Electromagnetic Theory. Hoboken, IEEE Press, 2007. 630 p.
Lurie A. I. Theory of Elasticity. Heidelberg, Springer-Verlag Berlin, 2005. 1050 p.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 O. О. Palchykov

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Authors who publish with this journal agree to the following terms:
1. Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work.




