Estimation of electrical resistivity of conductive materials of random shapes

Abstract

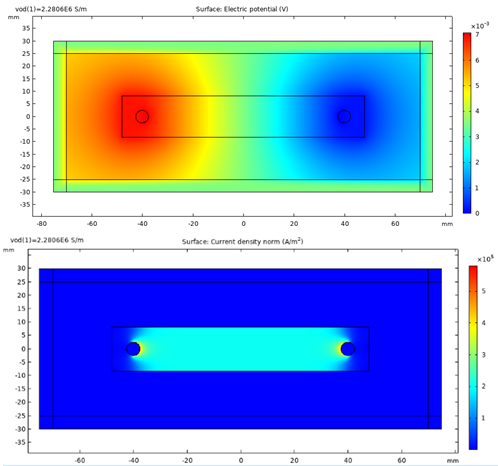
Introduction. Electrical resistivity is an important material characteristic in the field of electrical engineering and material science. There are several methods that can be used to measure resistance, like the 4-wire method which relates the resistance to a voltage drop at a given current flow, but to define the resistivity from the resistance value requires an analytical expression for the given system which requires a sufficient mathematical apparatus for describing complicated shapes. Therefore we use finite element method computations to compute the resistivity of a metal material. This approach has been already used for different materials like concrete and aluminum in the past. We then compare this method with an analytical expression that due to intuition could approximate the solution sufficiently. After that, the same material is used again to test the electrical isotropy of the sample. Novelty. A method is developed by combining the results of experimental studies and the results of mathematical modelling of the process of determining the electrical conductivity of metals. The goal is to describe and employ a method of measuring the electrical resistivity of metal objects of random shapes. Using this method, it is possible to measure the resistivity of materials without the need to manufacture them into wires or ribbons. Methods. The solution to the problem was carried out by the finite element method via the COMSOL Multiphysics 5.6 simulation program in a cartesian coordinate system and the resistance between two points of the metal sample was measured by the 4-wire method. Results. A similar resistance value was obtained when the measuring terminals were placed in different places. The difference between them was within 1,5 % and the obtained values were close to the values given by the literature for the electrical resistivity of electrical steels. Terminal size influences the measured conductivity and a max error of 5,2 % was estimated. Practical value. A method of estimating the resistivity of materials without the need to manufacture them into specific shapes, like wires or ribbons, for which analytical expressions between resistivity and resistance are easily derived.