Multi-objective optimal power flow based gray wolf optimization method
DOI:
https://doi.org/10.20998/2074-272X.2022.4.08Keywords:
optimization, power networks, optimal power flow, emission index, grey wolf optimizationAbstract
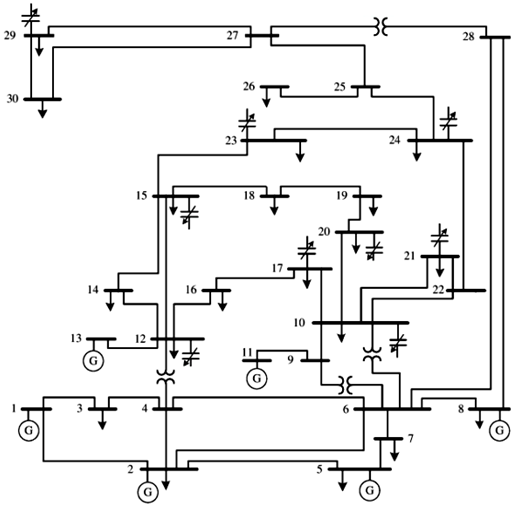
Introduction. One of predominant problems in energy systems is the economic operation of electric energy generating systems. In this paper, one a new evolutionary optimization approach, based on the behavior of meta-heuristic called grey wolf optimization is applied to solve the single and multi-objective optimal power flow and emission index problems. Problem. The optimal power flow are non-linear and non-convex very constrained optimization problems. Goal is to minimize an objective function necessary for a best balance between the energy production and its consumption, which is presented as a nonlinear function, taking into account of the equality and inequality constraints. Methodology. The grey wolf optimization algorithm is a nature inspired comprehensive optimization method, used to determine the optimal values of the continuous and discrete control variables. Practical value. The effectiveness and robustness of the proposed method have been examined and tested on the standard IEEE 30-bus test system with multi-objective optimization problem. The results of proposed method have been compared and validated with hose known references published recently. Originality. The results are promising and show the effectiveness and robustness of proposed approach.
References
Dommel H., Tinney W. Optimal Power Flow Solutions. IEEE Transactions on Power Apparatus and Systems, 1968, vol. PAS-87, no. 10, pp. 1866-1876. doi: https://doi.org/10.1109/TPAS.1968.292150.
Talaq J.H., El-Hawary F., El-Hawary M.E. A summary of environmental/economic dispatch algorithms. IEEE Transactions on Power Systems, 1994, vol. 9, no. 3, pp. 1508-1516. doi: https://doi.org/10.1109/59.336110.
Nicholson H., Sterling M.H. Optimum Dispatch of Active and Reactive Generation by Quadratic Programming. IEEE Transactions on Power Apparatus and Systems, 1973, vol. PAS-92, no. 2, pp. 644-654. doi: https://doi.org/10.1109/TPAS.1973.293768.
Santos A.Jr., da Costa G.R.M. Optimal-power-flow solution by Newton’s method applied to an augmented Lagrangian function. IEE Proceedings - Generation, Transmission and Distribution, 1995, vol. 142, no. 1, pp. 33-36. doi: https://doi.org/10.1049/ip-gtd:19951586.
Giras T.C., Talukdar S.N. Quasi-Newton method for optimal power flows. International Journal of Electrical Power & Energy Systems, 1981, vol. 3, no. 2, pp. 59-64. doi: https://doi.org/10.1016/0142-0615(81)90010-7.
Stott B., Hobson E. Power System Security Control Calculations Using Linear Programming, Part I. IEEE Transactions on Power Apparatus and Systems, 1978, vol. PAS-97, no. 5, pp. 1713-1720. doi: https://doi.org/10.1109/TPAS.1978.354664.
Sasson A. Nonlinear Programming Solutions for Load-Flow, Minimum-Loss, and Economic Dispatching Problems. IEEE Transactions on Power Apparatus and Systems, 1969, vol. PAS-88, no. 4, pp. 399-409. doi: https://doi.org/10.1109/TPAS.1969.292460.
Capitanescu F., Glavic M., Ernst D., Wehenkel L. Interior-point based algorithms for the solution of optimal power flow problems. Electric Power Systems Research, 2007, vol. 77, no. 5–6, pp. 508-517. doi: https://doi.org/10.1016/j.epsr.2006.05.003.
Mouassa S., Bouktir T. Artificial Bee Colony Algorithm for Solving OPF Problem Considering the Valve Point Effect. International Journal of Computer Applications, 2015, vol. 112, no. 1, pp. 45-53. Available at: https://www.ijcaonline.org/archives/volume112/number1/19634-1208 (accessed 23 May 2021).
Zakaria Z., Rahman T.K.A., Hassan E.E. Economic load dispatch via an improved Bacterial Foraging Optimization. 2014 IEEE 8th International Power Engineering and Optimization Conference (PEOCO2014), 2014, pp. 380-385. doi: https://doi.org/10.1109/PEOCO.2014.6814458.
Lai L.L. Intelligent System Applications in Power Engineering: Evolutionary Programming and Neural Networks. Wiley Publ., 1998. 286 p.
Khazali A.H., Kalantar M. Optimal reactive power dispatch based on harmony search algorithm. International Journal of Electrical Power & Energy Systems, 2011, vol. 33, no. 3, pp. 684-692. doi: https://doi.org/10.1016/j.ijepes.2010.11.018.
Abd Elazim S.M., Ali E.S. Optimal Power System Stabilizers design via Cuckoo Search algorithm. International Journal of Electrical Power & Energy Systems, 2016, vol. 75, pp. 99-107. doi: https://doi.org/10.1016/j.ijepes.2015.08.018.
Yuryevich J., Kit Po Wong. Evolutionary programming based optimal power flow algorithm. IEEE Transactions on Power Systems, 1999, vol. 14, no. 4, pp. 1245-1250. doi: https://doi.org/10.1109/59.801880.
Abou El Ela A.A., Abido M.A., Spea S.R. Optimal power flow using differential evolution algorithm. Electric Power Systems Research, 2010, vol. 80, no. 7, pp. 878-885. doi: https://doi.org/10.1016/j.epsr.2009.12.018.
Abido M.A. Optimal Power Flow Using Tabu Search Algorithm. Electric Power Components and Systems, 2002, vol. 30, no. 5, pp. 469-483. doi: https://doi.org/10.1080/15325000252888425.
Jeon Y.-J., Kim J.-C. Application of simulated annealing and tabu search for loss minimization in distribution systems. International Journal of Electrical Power & Energy Systems, 2004, vol. 26, no. 1, pp. 9-18. doi: https://doi.org/10.1016/S0142-0615(03)00066-8.
Bhowmik A.R., Chakraborty A.K. Solution of optimal power flow using nondominated sorting multi objective gravitational search algorithm. International Journal of Electrical Power & Energy Systems, 2014, vol. 62, pp. 323-334. doi: https://doi.org/10.1016/j.ijepes.2014.04.053.
Yaşar C., Özyön S. A new hybrid approach for nonconvex economic dispatch problem with valve-point effect. Energy, 2011, vol. 36, no. 10, pp. 5838-5845. doi: https://doi.org/10.1016/j.energy.2011.08.041.
Abido M.A. Optimal power flow using particle swarm optimization. International Journal of Electrical Power & Energy Systems, 2002, vol. 24, no. 7, pp. 563-571. doi: https://doi.org/10.1016/S0142-0615(01)00067-9.
Ketabi A., Alibabaee A., Feuillet R. Application of the ant colony search algorithm to reactive power pricing in an open electricity market. International Journal of Electrical Power & Energy Systems, 2010, vol. 32, no. 6, pp. 622-628. doi: https://doi.org/10.1016/j.ijepes.2009.11.019.
Padaiyatchi S.S. Hybrid DE/FFA algorithm applied for different optimal reactive power dispatch problems. Australian Journal of Electrical and Electronics Engineering, 2020, vol. 17, no. 3, pp. 203-210. doi: https://doi.org/10.1080/1448837X.2020.1817233.
Attia A.-F., El Sehiemy R.A., Hasanien H.M. Optimal power flow solution in power systems using a novel Sine-Cosine algorithm. International Journal of Electrical Power & Energy Systems, 2018, vol. 99, pp. 331-343. doi: https://doi.org/10.1016/j.ijepes.2018.01.024.
Ghasemi M., Ghavidel S., Ghanbarian M.M., Gharibzadeh M., Azizi Vahed A. Multi-objective optimal power flow considering the cost, emission, voltage deviation and power losses using multi-objective modified imperialist competitive algorithm. Energy, 2014, vol. 78, pp. 276-289. doi: https://doi.org/10.1016/j.energy.2014.10.007.
Mohamed A.-A.A., Mohamed Y.S., El-Gaafary A.A.M., Hemeida A.M. Optimal power flow using moth swarm algorithm. Electric Power Systems Research, 2017, vol. 142, pp. 190-206. doi: https://doi.org/10.1016/j.epsr.2016.09.025.
El-Hana Bouchekara H.R., Abido M.A., Chaib A.E. Optimal Power Flow Using an Improved Electromagnetism-like Mechanism Method. Electric Power Components and Systems, 2016, vol. 44, no. 4, pp. 434-449. doi: https://doi.org/10.1080/15325008.2015.1115919.
Mezhoud N., Ayachi B., Bahri A. Wind Driven Optimization Approach based Multi-objective Optimal Power Flow and Emission Index Optimization. International Research Journal of Multidisciplinary Technovation, 2022, pp. 21-41. doi: https://doi.org/10.54392/irjmt2223.
Hasan F., Kargarian A., Mohammadi A. A Survey on Applications of Machine Learning for Optimal Power Flow. 2020 IEEE Texas Power and Energy Conference (TPEC), 2020, pp. 1-6. doi: https://doi.org/10.1109/TPEC48276.2020.9042547.
Akbari E., Ghasemi M., Gil M., Rahimnejad A., Andrew Gadsden S. Optimal Power Flow via Teaching-Learning-Studying-Based Optimization Algorithm. Electric Power Components and Systems, 2021, vol. 49, no. 6–7, pp. 584-601. doi: https://doi.org/10.1080/15325008.2021.1971331.
Mohamed A.-A.A., El-Gaafary A.A.M., Mohamed Y.S., Hemeida A.M. Multi-objective Modified Grey Wolf Optimizer for Optimal Power Flow. 2016 Eighteenth International Middle East Power Systems Conference (MEPCON), 2016, pp. 982-990. doi: https://doi.org/10.1109/MEPCON.2016.7837016.
Dilip L., Bhesdadiya R., Trivedi I., Jangir P. Optimal Power Flow Problem Solution Using Multi-objective Grey Wolf Optimizer Algorithm. In: Hu Y.C., Tiwari S., Mishra K., Trivedi M. (eds) Intelligent Communication and Computational Technologies. Lecture Notes in Networks and Systems, 2018, vol. 19. Springer, Singapore. doi: https://doi.org/10.1007/978-981-10-5523-2_18.
Ayachi B., Boukra T., Mezhoud N. Multi-objective optimal power flow considering the multi-terminal direct current. Electrical Engineering & Electromechanics, 2021, no. 1, pp. 60-66. doi: https://doi.org/10.20998/2074-272X.2021.1.09.
Pradhan M., Roy P.K., Pal T. Grey wolf optimization applied to economic load dispatch problems. International Journal of Electrical Power & Energy Systems, 2016, vol. 83, pp. 325-334. doi: https://doi.org/10.1016/j.ijepes.2016.04.034.
El-Fergany A.A., Hasanien H.M. Single and Multi-objective Optimal Power Flow Using Grey Wolf Optimizer and Differential Evolution Algorithms. Electric Power Components and Systems, 2015, vol. 43, no. 13, pp. 1548-1559. doi: https://doi.org/10.1080/15325008.2015.1041625.
Lee K.Y., El-Sharkawi M.A. (Eds.). Modern Heuristic Optimization Techniques. John Wiley & Sons, Inc., 2008. 586 p. doi: https://doi.org/10.1002/9780470225868.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2022 N. Mezhoud, B. Ayachi, M. Amarouayache

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Authors who publish with this journal agree to the following terms:
1. Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
2. Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
3. Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work.




